A Toy Model of the Greenhouse Effect

Sometimes it's fun to build a "toy" model of how something should work just to see if a known effect can be modeled and understood, however approximately.  Here, I'll try to trace some very simple calculations (all of which have certainly been done very well elsewhere) just as a personal exercise to try to understand the order-of-magnitude effect of "heat-trapping" by an IR-absorbing gas like \(\text{CO}_2\).

The idea is to appeal to the basic physics of energy conservation.  Whatever energy the Earth gets from the Sun must be re-radiated out into space for the temperature to be in some sort of rough equilibrium.  The first step, then, is to calculate how much energy we actually receive from the Sun; I suppose the zeroth step is to calculate how much energy the Sun actually emits.

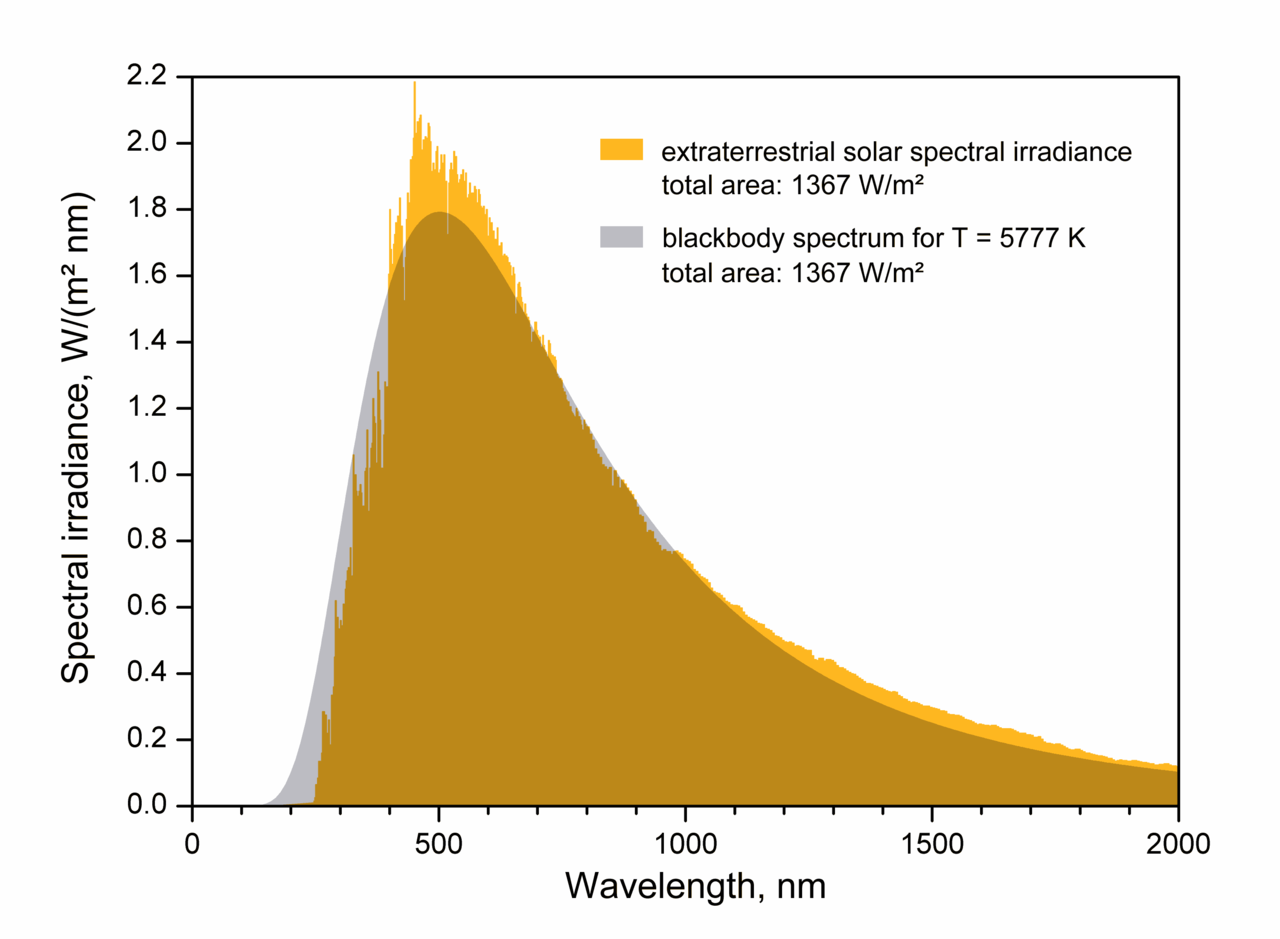Spectrum of the Sun, matched by a blackbody at about 5800 K

By looking at the spectrum of the Sun above, we see that it glows as an approximate blackbody with an effective ("surface") temperature of about 5800 K.  The amount of energy generated per second (the luminosity) then depends (sensitively!) on this temperature as well as how big the emitter (Sun) is:
\[L_{\odot}=\sigma A T^4=4\pi R_s^2 \sigma T_s^4 \approx 4\times 10^{26}\;\text{Watts}\]
Then we imagine that this total energy, emitted uniformly in all directions, is spread out around the inside of a gigantic sphere extending all the way out to the Earth's distance from the Sun.  Since the imaginary sphere completely wraps around the Sun, we know that it absorbs all the Sun's energy; in particular, each square meter of the surface absorbs only a tiny fraction of the total luminosity --- we just divide by the total surface area of the sphere to get the solar flux \(F_{\odot}\) of luminosity through each square meter:
\[F_{\odot}=\frac{L_{\odot}}{4\pi D_s^2} \approx 1400\;\text{Watts/m}^2\]
where \(D_s\) is the radius of this big sphere, which is the distance from the Earth to the Sun (\(1.5\times 10^{11}\) meters).  So, in principle, each square meter directly facing the Sun receives this much energy per second.  The problem is that not every square meter on the surface of the Earth points at the Sun --- close to the equator this is a pretty good approximation, but at the poles the sunlight is much more indirect.  One easy way out of a complex calculation is to imagine some sort of projection screen behind the Earth, where it's easy to realize that the total amount of sunlight blocked is just the same as the area of Earth's shadow, which is a circle.  So then the Earth intercepts an amount of sunlight equal to
\[(F_{\odot})(\pi R_e^2)\]
where \(R_e\) is the radius of the Earth.  Actually, this is still not quite right.  Not all the solar energy falling on the Earth is absorbed; some of it is reflected back into space by the surface, atmosphere, and clouds.  The percentage reflected back is called the albedo, and for the Earth an average value is about \(a=0.30\).  So that means that only about \((1-a)F_{\odot}\) reaches the surface and warms the planet.  The expression, then, for the solar radiation \(S\) warming the Earth is
\[S=(1-a)F_{\odot}\pi R_e^2\]
Finally, let's invoke the physics of energy balance --- if the Earth receives that much energy, and it's in equilibrium, it must radiate that much energy as well, and it radiates over it's entire spherical surface area.  So now we just make the Earth a radiator just as we did for the Sun to begin with:
\[(1-a)(F_{\odot})(\pi R_e^2) = \sigma (4\pi R_e^2) T_e^4\]
Now we can solve for the effective (radiative) temperature of the Earth!  Simplifying,
\[T_e = \left[\frac{(1-a)F_{\odot}}{4\sigma}\right]^{\frac{1}{4}} \approx 256\;\text{K}\]
after plugging in the numbers.  The effective temperature is sensitive to high albedo, as you can see in the plot below.  A perfectly absorbing (black) Earth would have a temperature of 280 K; however, a highly reflective Earth (perhaps covered in snow/ice) would be far cooler.  That most likely had significant effects in Earth's past.

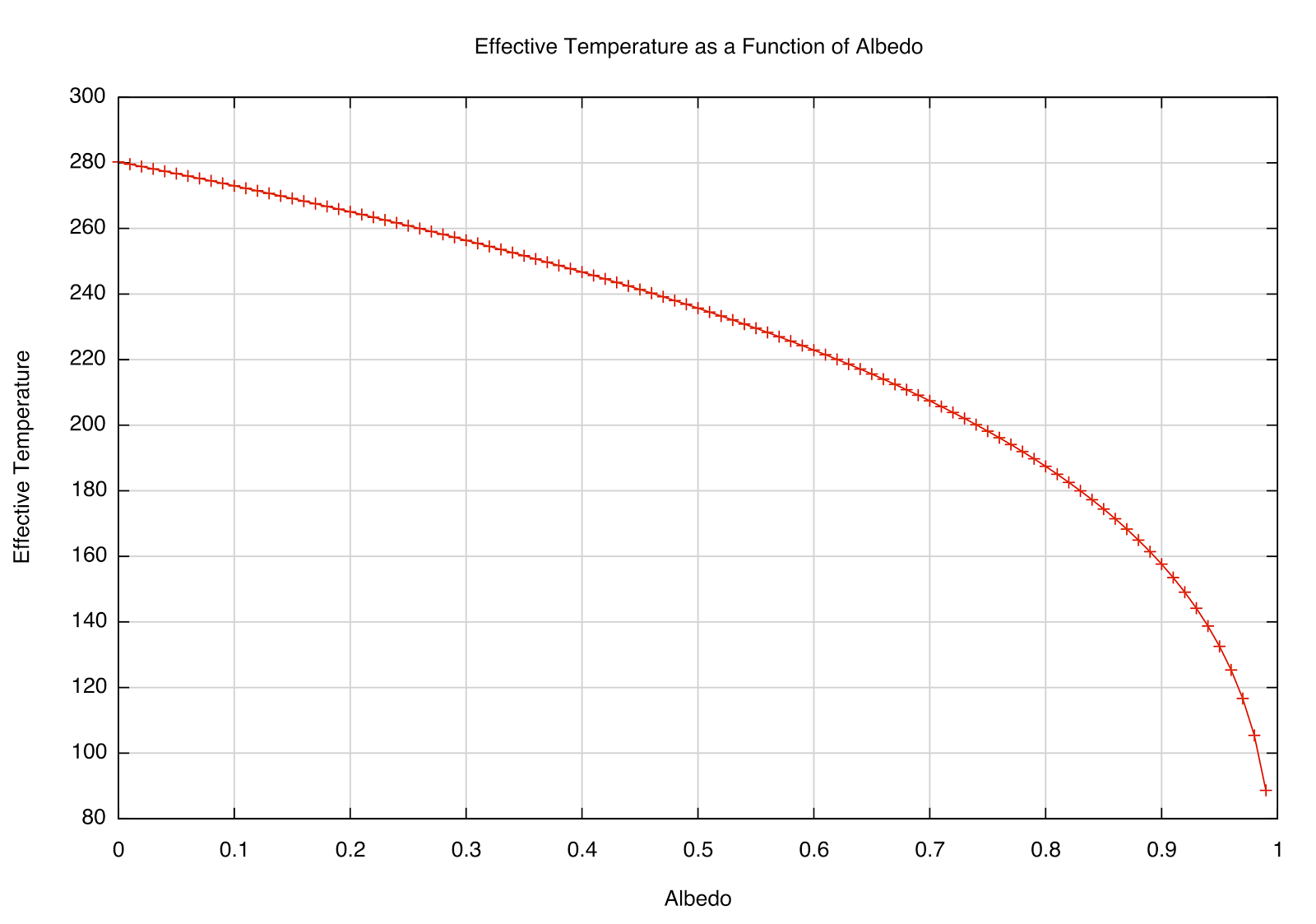How the \(T_e\) depends on reflectivity (albedo) of a planet at the Earth's distance from the Sun.

Since 273 Kelvins is the point where water freezes, an average temperature of 250 K is a little strange --- it's hard to imagine much liquid water on the surface if the average temperature around the globe is below \(0^{\circ}\)F!  What we've really done is calculate the temperature of a bare rock without accounting for any action of an atmosphere.

One simple way to model an absorbing atmosphere is to imagine a single layer that is transparent to the Sun's visible radiation, but absorbs infrared radiation (heat) emitted from the ground.  A schematic is below:

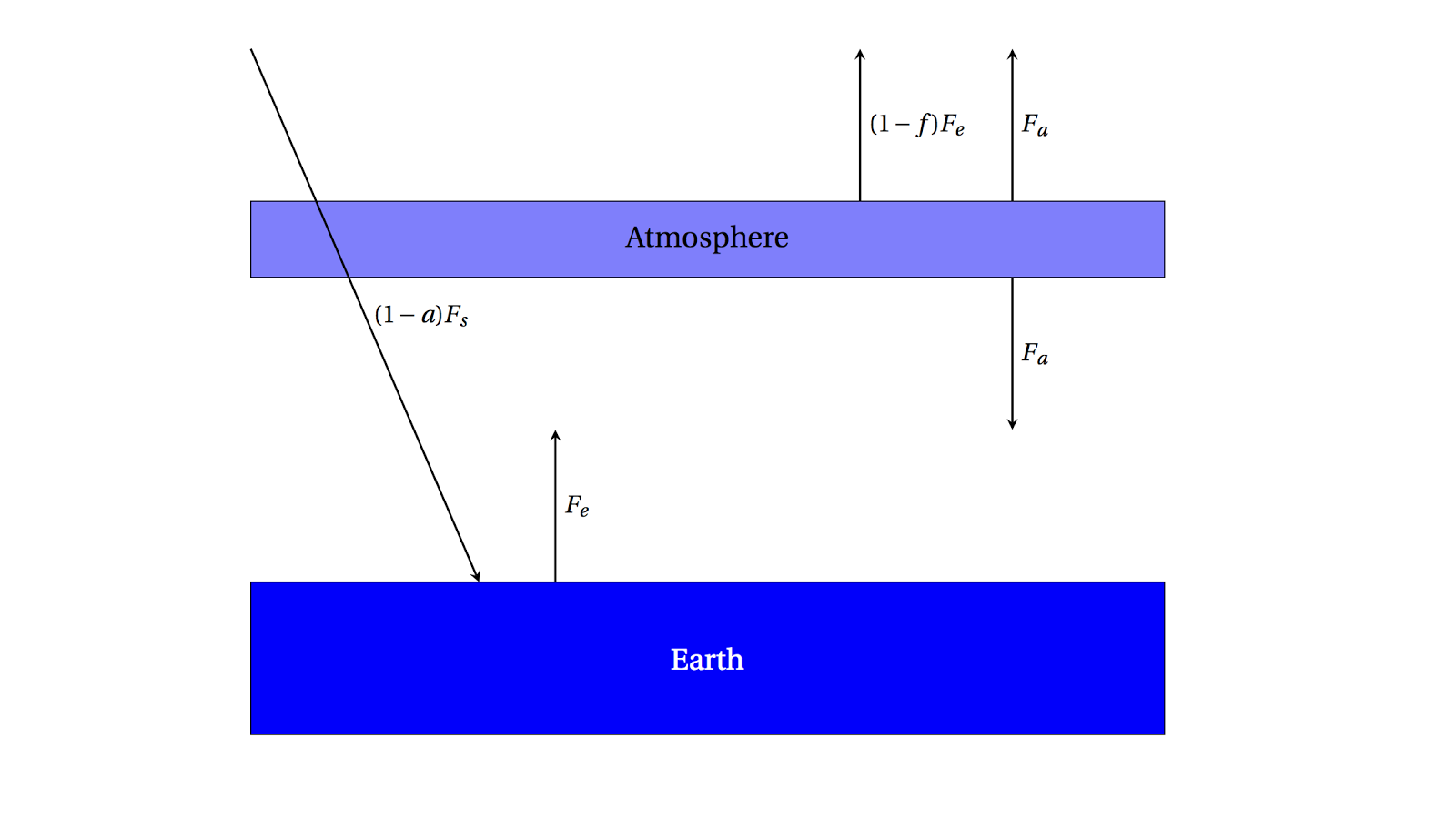A single-layer absorbing atmosphere model.

Radiation from the Sun \((1-a)F_s\) passes through the atmosphere and warms the ground, which emits \(F_e\) as we've found.  This radiation, though, is partially absorbed on the way out to space by the atmosphere by the fraction \(f\).  \((1-f)F_e\) can then escape to space, but the radiation emitted by the atmosphere is \(F_a\) in both directions.

Now we can write a new set of energy balance equations:  for the radiation escaping to space,
\[F_s = (1-f)F_e + F_a\]
which, in words, means that the radiation coming in from the Sun has to equal the amount emitted by the Earth, which is composed of both the amount absorbed and then emitted by the atmosphere as well as the amount emitted by the Earth that is not absorbed by the atmosphere.  Also, we can write
\[fF_e = 2F_a\]
for the atmosphere itself --- the amount of radiation from the Earth that is absorbed must be equal to the total amount emitted (in both directions, so we multiply by 2).  Then we can solve for \(F_e\)
\[F_s = (1-f)F_e + \frac{f}{2}F_e = (1-\frac{f}{2})F_e\]
\[\Rightarrow F_e = \frac{F_s}{1-\frac{f}{2}}\]
and since, from before, \(F_e = \sigma T_e^4\), and plugging in what we had for \(F_s\),
\[T_e = \left[\frac{(1-a)F_s}{\left(1-\frac{f}{2}\right)4\sigma} \right]^{\frac{1}{4}}\]
This dependence of \(T_e\) on the absorption fraction \(f\) is plotted below:

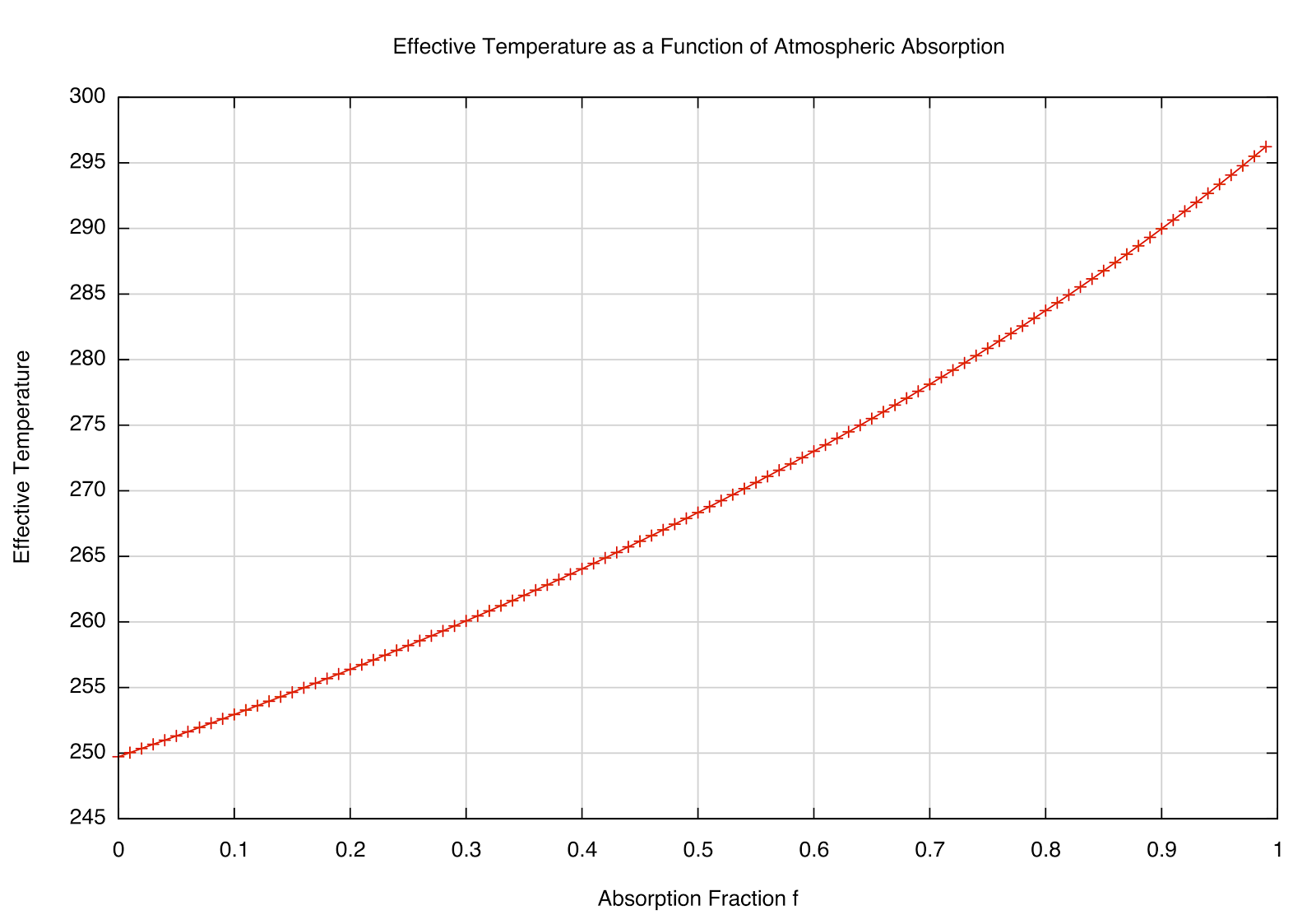How the \(T_e\) varies as the absorption fraction of the atmosphere.

This makes sense --- if \(f=0\), we're back to the "bare rock" we had before (no atmosphere), but interestingly, if \(f=1\) (totally absorbing), we get \(F_e = 2F_s\), and a temperature of about 297 K.  The observed global mean temp is about 288 K, meaning that the atmosphere absorbs about 85% of the infrared radiation emitted by the Earth (according to our very simple model and rounding off some numbers).  We can also solve for \(T_a\), which would be the emission temperature at the top of the atmosphere --- that works out to be about 240 K for the simple model (roughly what we actually see at the top of the troposphere) and about 210 K for more detailed models taking into account the changing density of the atmosphere at different elevations.  This is interesting --- since the amount of radiation from the Sun doesn't change much, then if the lower atmosphere is heating, the upper atmosphere should be cooling to compensate.

One of the utilities of toy models like this is to get a feel for how the physics works.  For example, one objection I've heard to the idea that increasing concentrations of greenhouse gases will continue to warm the planet is that, since they absorb already a large fraction of outgoing radiation, adding to it doesn't further increase the temperature.  This may at first sound reasonable, but it ignores the physical model of what's really happening --- it's not just that the gases trap the heat, but they re-radiate it.  Let's suppose, just to make the point, that \(f=1\) in our atmosphere, so that it is perfectly absorbing.  What happens when we insert another layer of such an atmosphere?  This would look something like this plot:

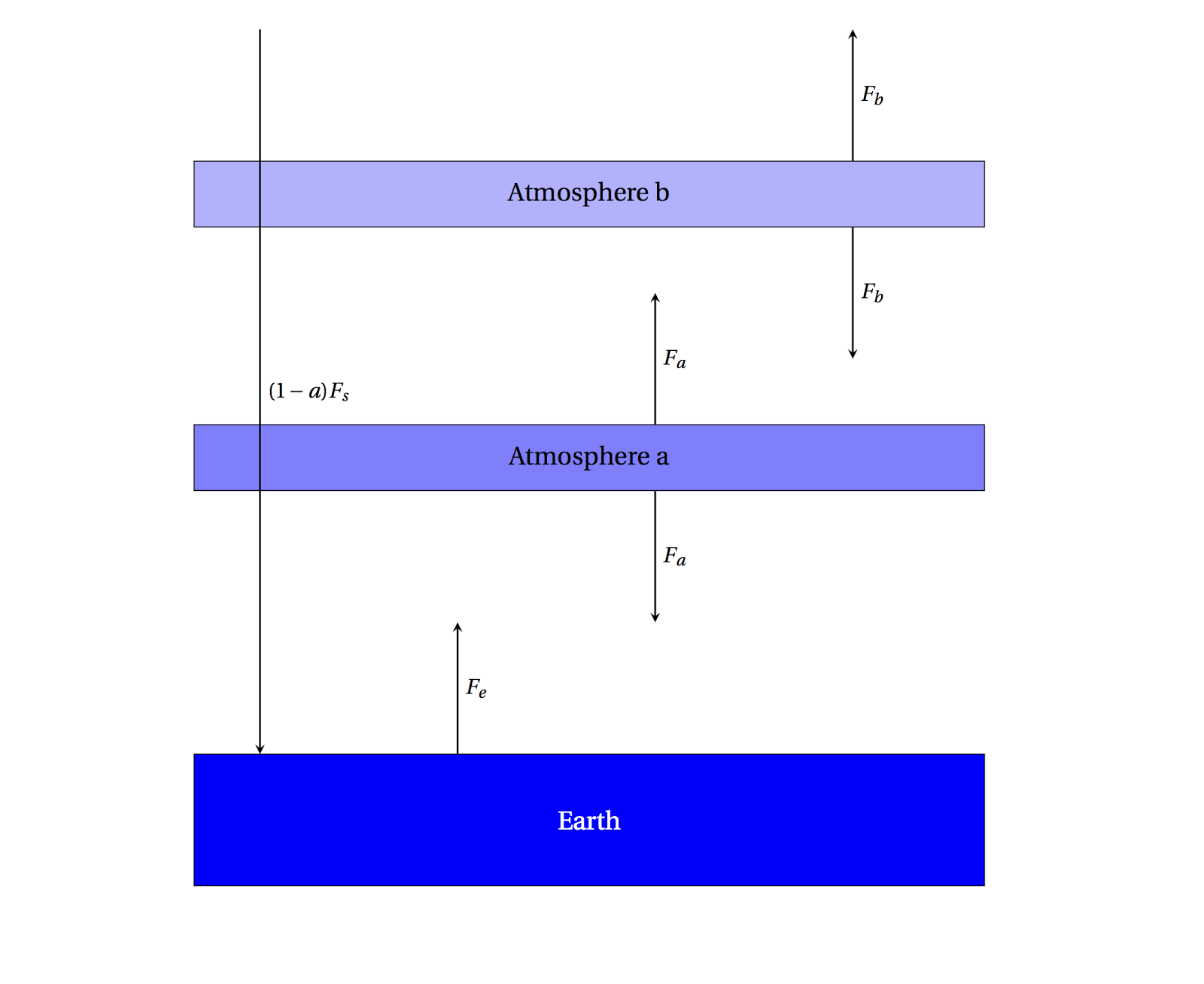A 2-layer simple atmosphere, perfectly absorbing the outgoing radiation.

Now setting up the energy balance equations looks like
\[F_e + F_b = 2F_a\;\text{for Atmosphere a}\]
\[F_a = 2F_b\;\text{for Atmosphere b}\]
\[F_s = F_b\;\text{incoming/outgoing}\]
then
\[F_e + F_b = 4F_b\]
\[F_e = 3F_b = 3F_s\]
This is the same as what we had before in the \(f=1\) case, only there is a factor of 3 instead of 2 before, so you can compute that \(T_e=329\) K.  Note that the Earth's radiation was already absorbed, but adding more greenhouse gas has the effect of further absorbing the radiation emitted by the first layer.